11. 三角形の魔法
三角形は最小の多角形です。この三角形には、幾つかの魔法が秘められています。
多角形とは、複数の線が交差しないように形つくられたものです。
1. 三角形の特徴
代表的な三角形を三つ示します。
① 正三角形
正三角形は、三辺の辺の長さが同じ三角形のことです。その特徴は、三つの内角が60度で同じです。三角形の内角の総和は360度となります。度の記号は°です。
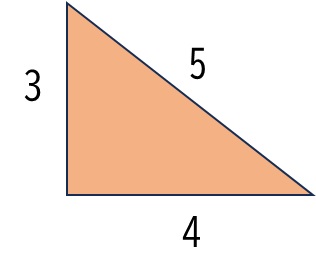
② 三辺の整数比が3、4、5の直角三角形
三辺の整数比を3,4.、5にしますと、辺の長さが3と4で交差する角度が90度になります。
これは、今から2500年ほど前にピタゴラスが発見したといわれているピタゴラスの定理(三平方の定理)が適用されます。この定理の計算式は、a2+b2=c2です。
この式に上記の三つの数字を入れてみます。32+42=52となり、ピタゴラスの定理が成立します。
直角の線を引きたい場合は、コンパスがなくても、紐を整数比3、4、5で出来た直角三角形を活用することができます。
③ 多角形は三角形の集合体
多角形は三角形の集合体です。これを五角形で示します。
五角形の中にある一点を決めて、その点から放射状に五つの角に線を引きます。すると、五角形の中に三角形が五つできます。五角形は五個の三角形の集合体となります。

この五角形の五つの内角の総和を求めて見ましょう。
(五つの三角形の内角の総和)-(中にある点は円なので、円の角度)
=(5✕180)-360
=900-360
=540
五角形の内角の総和は540度となります。
上記の式から多角形の内角の総和を導き出す計算式を考えてみます。五角形の計算式を少し、変形します。
(五つの三角形の内角の総和)-(中にある点の円周の角度)
=(5✕180)-360
=(5✕180)-2✕180
=(5-2)✕180
この式からn角形の内角の総和の式は次のようになります。
(n-2)✕180
この計算式を使って内角の総和を計算してみます。
三角形は180度
四角形は360度
五角形は540度 となります。
一つ角が増えますと、三角形が一つ増えたことになるのと同じ事になります。
2. 数字3の特徴
数字三の特徴は、前記の三角形の特徴が基になります。
① まとまる、覚えやすい
一角形や二角形の形は存在しません。三角形になってから、一つの形となってまとまります。
物事を三つにしますとまとめやすく、覚えやすいです。
② 発展する、展開する
三角形は、最小の多角形ですので、四角形・五角形へと無限に発展します。
数字三は、物事を発展する、展開するにつながります。
③ 調和がとれる、安定する
生け花などで、天地人の形があるそうです。これは、天は高い花、地は低い花、人は中ぐらいの高さの花をさします。これが、調和が取れる形となります。
その他に、人の関係でも、三人いますと、話や権力が偏らず互いに牽制して調和がとれたり、安定します。
三脚は、三本の足で最上部を一点で交わらせたものです。その上にカメラなどを支える台をおきます。写真を安定して撮ることができます。
3. 生活の中における数字三の存在
生活の中において、数字の三を含んだ言葉や物事を三つにまとめて表現する言葉もあります。これを大雑把に三つに分けて例示します。
① 三文字の熟語
三つの事柄を一つの熟語にする三文字熟語があります。例をいくつか示します。
上中下
大中小
朝昼晩
松竹梅
心技体
② 三語で一つの意味を表わす言葉
空間の座標軸 縦、横、高さ
時間の流れ 過去、現在、未来
三権分立 立法(国会)、行政、司法(裁判所)
三種の神器 鏡、剣、曲玉
現実主義 現場、現物、現実
③ 三がつく諺などの言葉
三つ子の魂百まで
早起きは三文の徳
石の上にも三年
三人寄れば文殊の知恵
桃栗三年柿八年柚の馬鹿めが十三年
